Randomness has always been part of Axie Infinity's core gameplay. From V2 to Origin, the heat of the battle lives on with some element of randomness. Although the crit system, which is one of the main sources of randomness in the game, will have to say goodbye in Axie Infinity: Origin. New sources of randomness emerge. One of them is the Kotaro card:
The description says: “Deal 2 hits to random enemies. Gain 1 energy if hit at least 2 enemies“. So the chance of us gaining extra energy is based on those two random hits. If we can compute the exact value of their probabilities, it would really help us to properly time our attack to get that extra energy. In this article, we will compute those probabilities using some basics of Probability Theory.
Spoiler!
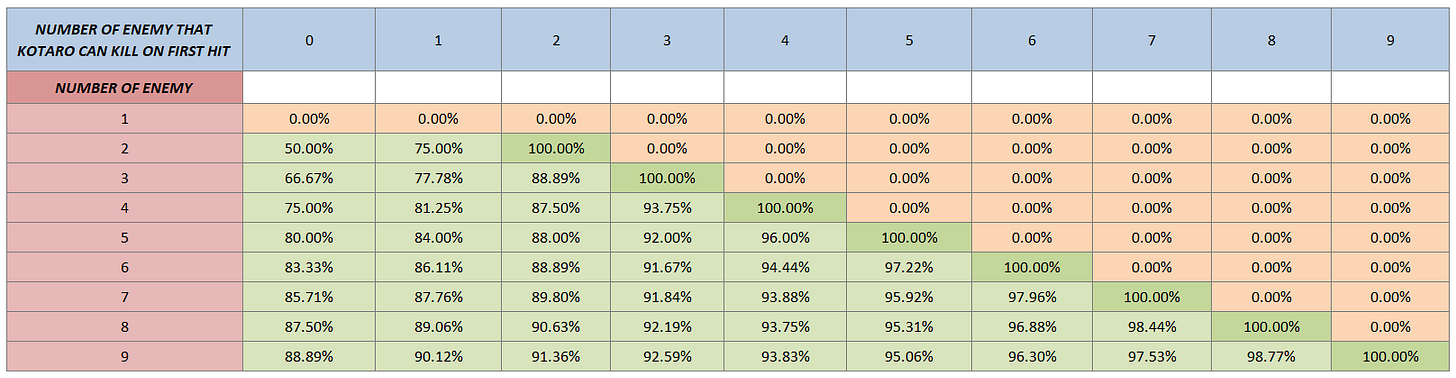
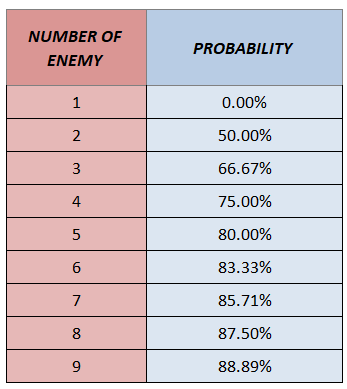
If you are not interested in the computation, here are some numbers:
Here’s a more complete breakdown of numbers:
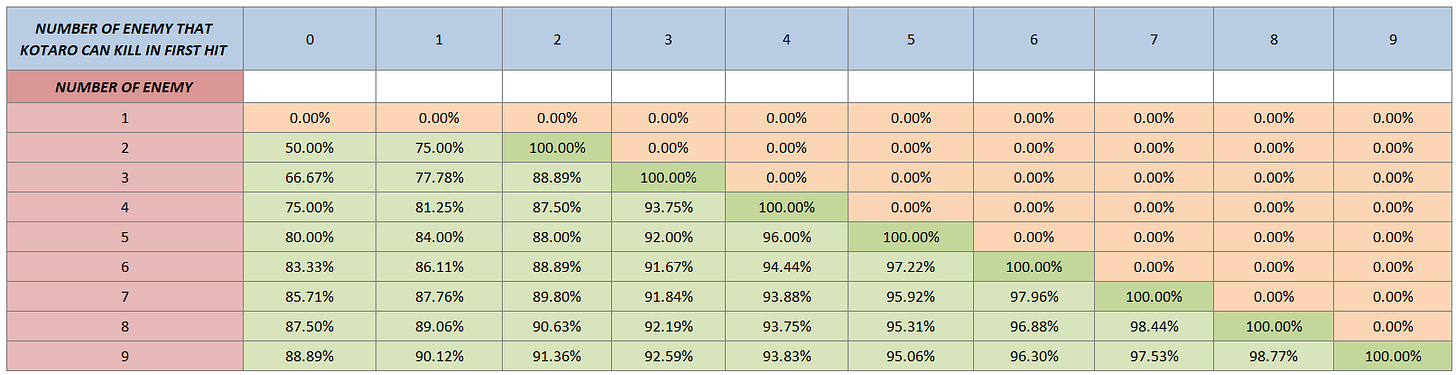
Note how the probability depends on the number of enemies that Kotaro has a chance to kill during its first hit. From the table, we can say that timing your combo to last hit an opponent during Kotaro’s first hit, improve your chances of getting that extra energy.
Here’s an excel calculator tool:
Note: All contents are free to use as long as proper reference/credit is in place. Feel free to send corrections if you found one. twitter account: @alvinaragoneth
What is Probability
Before moving on with the case of the Kotaro card, let’s discuss first some basics. Let’s start with an intuitive definition of probability and an example:
Probability is the likely hood of something to occur.
Example
Imagine we’re in Round 1 of an Axie V2 game, and we want to get the likely hood of the following to occur:
A: Chance of drawing up a mouth card or a tail card
B: Chance of drawing up six mouth cards
C: Chance of drawing up an ear card
Using our intuition to judge the likely hood of these events:
A will likely happen.
B will be less likely to happen.
C will never happen.
But this level of measurement of likely, less likely, and highly likely is not accurate enough for us to fully assess the likely hood of these events. So we will level up our definition of probability.
Let’s Reinterpret Probability
Some definitions first before we move on:
Trial - is a procedure that have well-defined outcomes.
An example of a trial is the procedure of selecting a part on this axie:
This is a trial since selecting a part would lead to definite outcomes. And the outcomes are:
{ Mavis, Curly, Hero, Axie Kiss, Dual Blade, Hare }
This set of all outcomes is called sample space.
Let’s select a subset of this set:
{ Hero, Axie Kiss, Dual Blade, Hare }
Note that this subset can be described in words as:
Parts of the axie that are beast class.
This subset is called an event.
So when we ask about the probability of something, we are actually asking what is the probability of an event given a trial.
So for the event above: “Parts of the axie that are beast class”, the probability of this event means the probability of selecting a beast part of the axie.
Reinterpreting The Kotaro Case
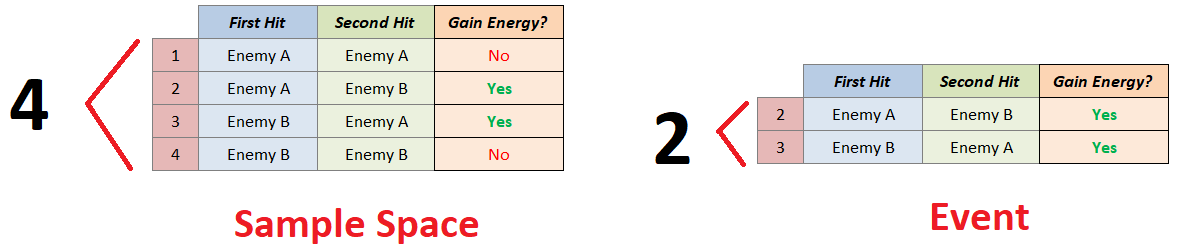
Let’s try this reinterpretation with the Kotaro Case. Let’s start with the case where we have 2 enemies. Our goal is to reinterpret the following probability:
Probability of gaining extra energy using Kotaro card if we have 2 enemies.
Let’s start by identifying what is our trial, sample space, and event:
Trial:
Hit two enemies randomly.
Sample Space:
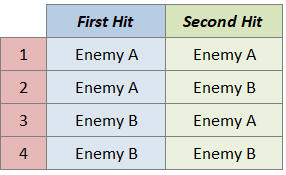
If we name our enemies: Enemy A and Enemy B, these are the possible outcomes:
We have 4 possible outcomes. This set is our sample space.
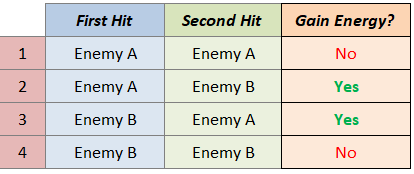
Event:
Now, let’s identify which of these outcomes lets us gain 1 extra energy. Note that we gain 1 energy if we hit two different enemies.
Getting all outcomes that give us energy, will give us our event. Our event would then be this subset:
Our reinterpretation of our Kotaro Case probability would then be the probability of the event above.
Computing The Probability
Finally, we can now compute the probability.
If each of the outcomes is equally likely to happen, then the probability of an event is given by the following formula:
In the Kotaro Case above where we have 2 enemies, our sample space has a total of 4 outcomes and our event has 2 outcomes:
Thus the probability of gaining extra energy using Kotaro card if we have 2 enemies is:
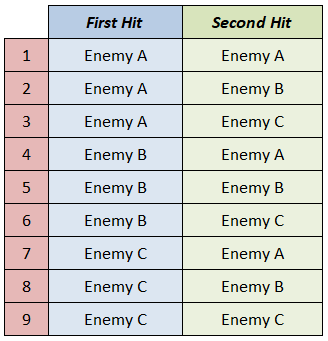
Computing The Case For 3 Enemies
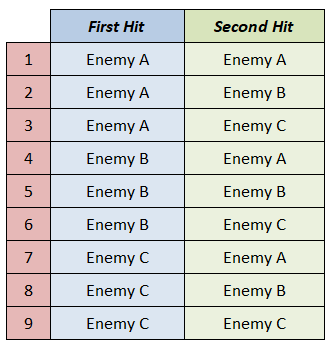
Now let’s try the case where we have 3 enemies. If our enemies are Enemy A, Enemy B, and Enemy C, then our sample space is:
We have 9 total outcomes.
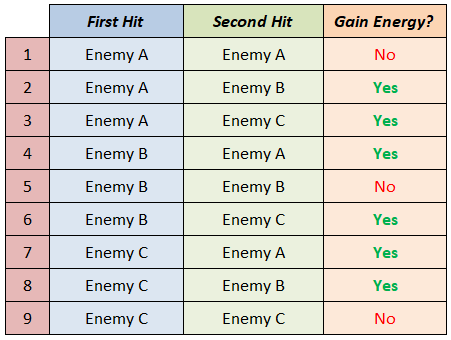
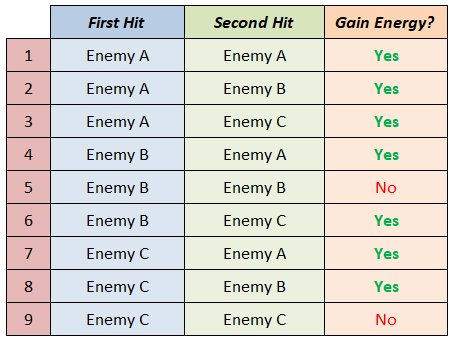
Identifying which of these outcomes lets us gain 1 extra energy.
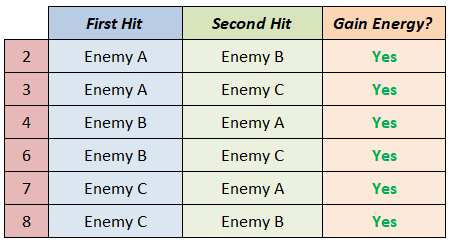
Our event then is:
We have 6 total outcomes.
Computing for the probability:
Now, unlike Axie V2 where we have a max of 3 enemies, Axie Origin may have more. This is due to the new summoning mechanics. So computing the probability for more than 3 enemies will also be an interest to us.
Here we already computed and compiled the complete probabilities from 1 to 9 enemies:
Last Hit! GameChanger
Now, all of our computation is based on the assumption that we didn’t kill the first enemy we hit. The probability actually changes if we do have a chance. Let’s check it for the case where we have 3 enemies.
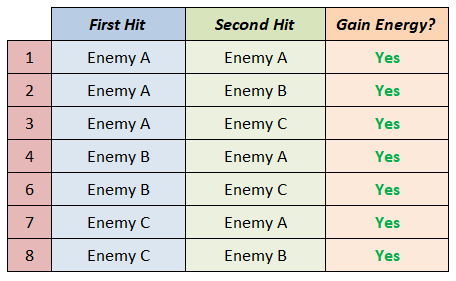
Let’s assume that our enemies are Enemy A, Enemy B, and Enemy C. Also let’s assume that Enemy A has lower than 30 HP or we can use some cards first to make Enemy A’s HP lower to 30 HP.
Our sample space is:
Note that the first outcome: Enemy A first hit and Enemy A second hit will never happen since we assume that we can kill Enemy A on the first hit. So we might wonder, why do we have to include it in our sample space. This is actually just a hack for the sake of this discussion. Removing it would require us to touch more advanced concepts like weighted probabilities which are beyond the scope of this article. For now, think of it as a placeholder.
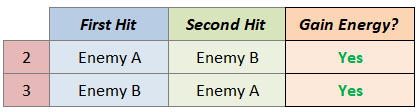
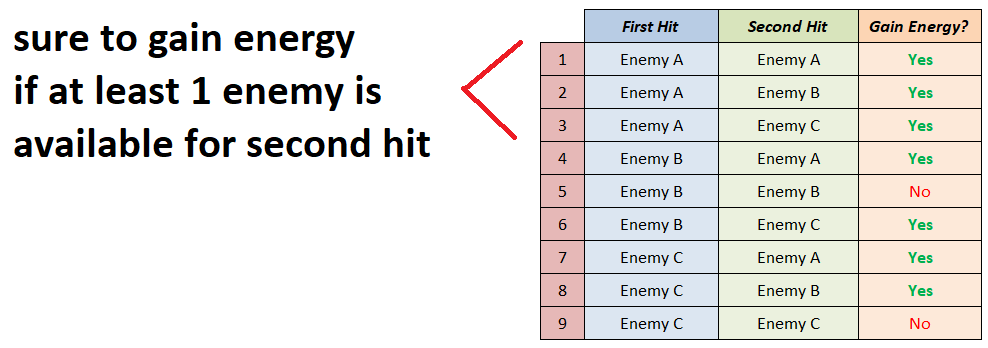
Identifying which of these outcomes lets us gain 1 extra energy.
Note that: if we hit Enemy A first, then as long as there’s an enemy to hit the second time around, we are guaranteed to gain extra energy. So we put yes in all cases of “first hit Enemy A”.
Our event then is:
We have 7 total outcomes.
Computing for the probability:
Things will also be different if we have a chance to last hit more than one enemy during the first hit of Kotaro. Here’s a summary of these probabilities:
One Formula to Rule Them All
Note that our method above is not the most efficient way of computing probability. If we are computing for the case of 9 enemies, we have to list down:
9 x 9 = 81
81 outcomes in a table. So I prepare the following formula:
The formula for computing the probability of gaining extra energy with n enemies and k potential enemies to kill at first hit is:
where n >= k and (if n = 1, k > 1). The probability of the rest of the case is 0.
The derivation of this formula is out of the scope of this article. Our only goal here is to introduce the concept of probability and get familiar with its basics. But if there’s enough demand, I will make a Part 2 exploring the computation behind the formula.
Closing Remarks
Hope this article helps you in some way understand the underlying probabilities surrounding the use of Kotaro card. If you find any consistency/error in this article or you have questions/clarifications, just comment below or hit me up on Twitter: @alvinaragoneth












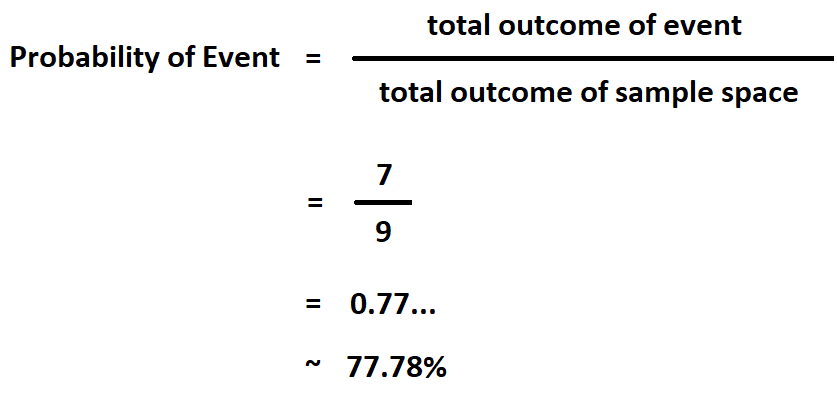
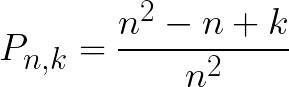
Umm if it not be like you think ? May be 2 hit in same time and not same enemy. We can gain 1 energy until the last one.